How To Analyze The Xps Spectra
XPS Spectra The XPS technique is used to investigate the chemistry at the surface of a sample. Figure 1: Schematic of an XPS instrument. The basic mechanism behind an XPS instrument is illustrated in Figure 1. Photons of a specific energy are used to excite the electronic states of atoms below the surface of the sample. XPS Basic Data Analysis MultiPak is a MatLab-based program with specific macros written by PHI to handle data reduction of both AES and XPS (ESCA) data. Once open on the desktop, MultiPak has a “Hide MultiPak”, “Show MultiPak” toggle feature that allows you to minimize and restore all the MultiPak windows simultaneously (FIG 1).
Description of Technique
X-Ray Photoelectron Spectroscopy (XPS), also known as Electron Spectroscopy for Chemical Analysis (ESCA), is an analysis technique used to obtain chemical information about the surfaces of solid materials. Both composition and the chemical state of surface constituents can be determined by XPS. Insulators and conductors can easily be analyzed in surface areas from a few microns to a few millimeters across.
The sample is placed in an ultrahigh vacuum environment and exposed to a low-energy, monochromatic x-ray source. The incident x-rays cause the ejection of core-level electrons from sample atoms. The energy of a photoemitted core electron is a function of its binding energy and is characteristic of the element from which it was emitted. Energy analysis of the emitted photoelectrons is the primary data used for XPS. When the core electron is ejected by the incident x-ray, an outer electron fills the core hole. The energy of this transition is balanced by the emission of an Auger electron or a characteristic x-ray. Analysis of Auger electrons can be used in XPS, in addition to emitted photoelectrons.
The photoelectrons and Auger electrons emitted from the sample are detected by an electron energy analyzer, and their energy is determined as a function of their velocity entering the detector. By counting the number of photoelectrons and Auger electrons as a function of their energy, a spectrum representing the surface composition is obtained. The energy corresponding to each peak is characteristic of an element present in the sampled volume. The area under a peak in the spectrum is a measure of the relative amount of the element represented by that peak. The peak shape and precise position indicates the chemical state for the element.
XPS is a surface sensitive technique because only those electrons generated near the surface escape and are detected. The photoelectrons of interest have relatively low kinetic energy. Due to inelastic collisions within the sample's atomic structure, photoelectrons originating more than 20 to 50 Å below the surface cannot escape with sufficient energy to be detected.
How To Analyze The Xps Spectra 1
Analytical Information
Survey Scan - Energy peaks in the survey scan identify the elemental composition of the uppermost 20 to 50 Å of the analyzed surface. All elements, except hydrogen and helium, are detected. Detection limits are approximately 0.1 atom percent for most elements.
High Resolution Multiplex Scan - This technique evaluates the chemical state(s) of each element through its core electron binding energies. Precise determinations of binding energies are made through the use of curvefitting routines applied to the peaks in the multiplex scan. Shifts in the binding energy can result from the atom’s oxidation state, chemical bonds, or crystal structure. A NIST database is available to identify binding energies with specific compounds.
Quantitation - The concentrations of the elements identified in the survey scan are determined by integrating the area under a characteristic peak for each element. Sensitivity factors are applied to the peak area values to determine the elemental concentration.
Depth Profile - The elemental composition is measured as a function of depth into the sample by alternating AES analysis with ion sputtering to remove material from the sample surface. Depth resolution of
Mapping - The relative concentration of one or more elements is determined as a function of lateral position on the sample surface. An image is obtained where brightness indicates the element concentration.
Typical Applications
- Analysis of thin film contamination
- Evaluation of adhesion failures
- Measurement of elemental composition of insulating materials (e.g., polymers, glasses)
- Identification of the chemical state of surface films (e.g., metal or oxide)
- Quantitative elemental depth profiling of insulators
Sample Requirements
Sample size cannot exceed 1 in. (25 mm) in any lateral direction. Height should not exceed ½ in. (12 mm). Sample must be compatible with an ultra-high vacuum environment (>10-9 Torr).
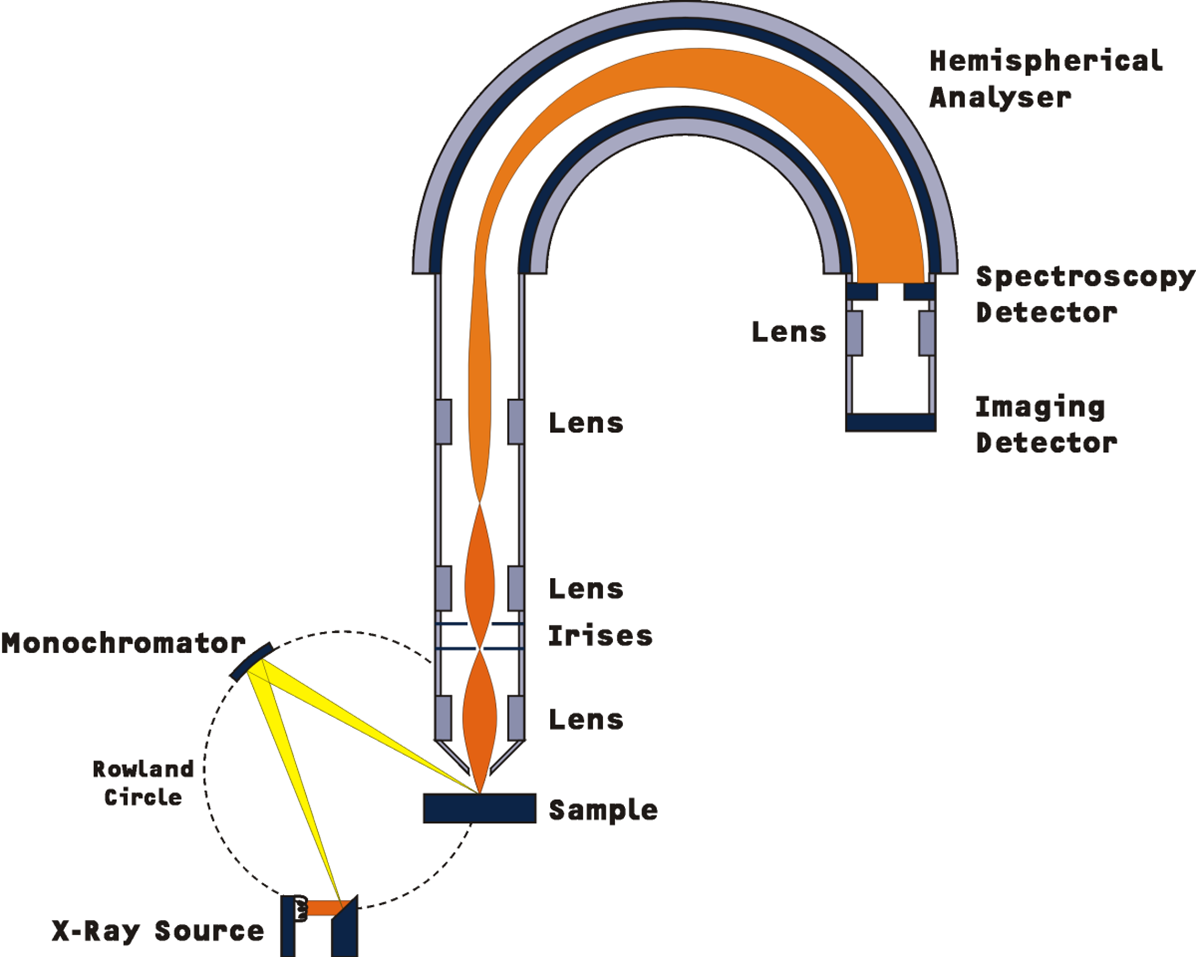
The basic mechanism behind an XPS instrument is illustrated in Figure 1. Photons of a specific energy are used to excite the electronic states of atoms below the surface of the sample. Electrons ejected from the surface are energy filtered via a hemispherical analyser (HSA) before the intensity for a defined energy is recorded by a detector. Since core level electrons in solid-state atoms are quantized, the resulting energy spectra exhibit resonance peaks characteristic of the electronic structure for atoms at the sample surface. While the x-rays may penetrate deep into the sample, the escape depth of the ejected electrons is limited. That is, for energies around 1400 eV, ejected electrons from depths greater than 10nm have a low probability of leaving the surface without undergoing an energy loss event, and therefore contribute to the background signal rather than well defined primary photoelectric peaks.
XPS Spectra The XPS technique is used to investigate the chemistry at the surface of a sample.
In principle, the energies of the photoelectric lines are well defined in terms of the binding energy of the electronic states of atoms. Further, the chemical environment of the atoms at the surface result in well defined energy shifts to the peak energies. In the case of conducting samples, for which the detected electron energies can be referenced to the Fermi energy of the spectrometer, an absolute energy scale can be established, thus aiding the identification of species. However, for non-conducting samples the problem of energy calibration is significant. Electrons leaving the sample surface cause a potential difference to exist between the sample and the spectrometer resulting in a retarding field acting on the electrons
Figure 1: Schematic of an XPS instrument.
1
Copyright © 2013 Casa Software Ltd. www.casaxps.com
escaping the surface. Without redress, the consequence can be peaks shifted in energy by as much as 150 eV. Charge compensation designed to replace the electrons emitted from the sample is used to reduce the influence of sample charging on insulating materials, but nevertheless identification of chemical state based on peak positions requires careful analysis.
The background in XPS is non-trivial in nature and results from all those electrons with initial energy greater than the measurement energy for which scattering events cause energy losses prior to emission from the sample. The zero-loss electrons constituting the photoelectric peak are considered to be the signal above the background approximation. A variety of background algorithms are used to measure the peak area; none of the practical algorithms are correct and therefore represent a source for uncertainty when computing the peak area. Peak areas computed from the background subtracted data form the basis for most elemental quantification results from XPS.
XPS is a quantitative technique in the sense that the number of electrons recorded for a given transition is proportional to the number of atoms at the surface. In practice, however, to produce accurate atomic concentrations from XPS spectra is not straight forward. The precision of the intensities measured using XPS is not in doubt; that is intensities measured from similar samples are repeatable to good precision. What may be doubtful are results reporting to be atomic concentrations for the elements at the surface. An accuracy of 10% is typically quoted for routinely performed XPS atomic concentrations. For specific carefully performed and characterised measurements better accuracy is possible, but for quantification based on standard relative sensitivity factors, precision is achieved not accuracy. Since many problems involve monitoring changes in samples, the precision of XPS makes the technique very powerful. The first issue involved with quantifying XPS spectra is identifying those electrons belonging to a given transition. The standard approach is to define an approximation to the background signal.
Figure 2: An example of a typical XPS survey spectrum taken from a compound sample.
2
Copyright © 2013 Casa Software Ltd. www.casaxps.com
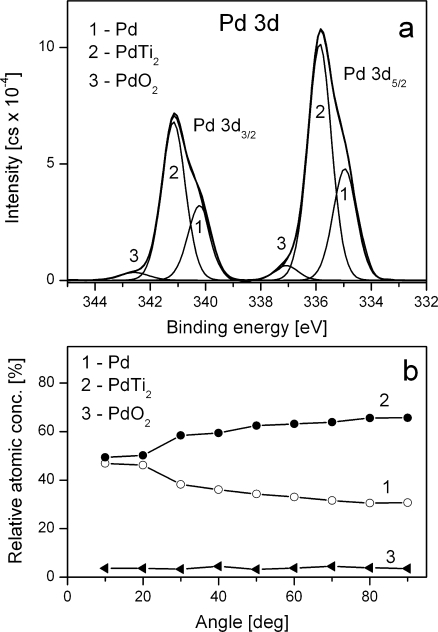
The data in Figure 2 illustrates an XPS spectrum measured from a typical sample encountered in practice. The inset tile within Figure 2 shows the range of energies associated with the C 1s and K 2p photoelectric lines. Since these two transitions include multiple overlapping peaks, there is a need to apportion the electrons to the C 1s or the K 2p transitions using a synthetic peak model fitted to the data. The degree of correlation between the peaks in the model influences the precision and therefore the accuracy of the peak area computation. Relative sensitivity factors of photoelectric peaks are often tabulated and used routinely to scale the measured intensities as part of the atomic concentration calculation. These RSF tables can only be accurate for homogenous materials. If the sample varies in composition with depth, then the kinetic energy of the photoelectric line alters the depth from which electrons are sampled. It is not uncommon to see evidence of an element in the sample by considering a transition at high kinetic energy, but find little evidence for the presence of the same element when a lower kinetic energy transition is considered. Transitions of this nature might be Fe 2p compared to Fe 3p both visible in Figure 2, where the relative intensity of these peaks will depend on the depth of the iron with respect to the surface. Sample roughness and angle of the sample to the analyser also changes the relative intensity of in-homogenous samples, thus sample preparation and mounting can influence quantification values.
Figure 3: Germanium Oxide relative intensity to elemental germanium measured using photoelectrons with kinetic energy in the range 262 eV to 272 eV.
Figure 4: Germanium Oxide relative intensity to elemental germanium measured using photoelectrons with kinetic energy in the range 1452 eV to 1460 eV.
3
Copyright © 2013 Casa Software Ltd. www.casaxps.com
The chemical shifts seen in XPS data are a valuable source of information about the sample. The spectra in Figure 3 and Figure 4 illustrate the separation of elemental and oxide peaks of germanium due to chemical state. Both spectra were acquired from the same sample under the same conditions with the exception that the ejected electrons for the Ge 3d peaks are about 1200 eV more energetic that the Ge 2p electrons. The consequence of choosing to quantify based on one of these transitions is that the proportion of oxide to elemental germanium differs significantly. The oxide represents an over layer covering of the elemental germanium and therefore the low energy photoelectrons from the Ge 2p line are attenuated resulting in a shallower sampling depth compared to the more energetic Ge 3d electrons. Hence the volume sampled by the Ge 2p transition favours the oxide signal, while the greater depth from which Ge 3d electrons can emerge without energy loss favours the elemental germanium. While these variations may seem a problem, such changes in the spectra are also a source for information about the sample.
layers; while at 90° the elemental substrate becomes dominant in the spectrum.
Tilting the sample with respect to the axis of the analyser results in changing the sampling depth for a given transition and therefore data collected at different angles vary due to the differing composition with depth. Figure 5 is a sequence of Si 2p spectra measured from the same silicon sample at different angles. The angles associated with the spectra are with respect to the axis of the analyser and the sample surface. Data measured at 30° favours the top most oxide
Figure 5: Angle resolved Si 2p spectra showing the changes to the spectra resulting from tilting the sample with respect to the analyser axis.
4
Copyright © 2013 Casa Software Ltd. www.casaxps.com
Other Peaks in XPS Spectra Not all peaks in XPS data are due to the ejection of an electron by a direct interaction with the incident photon. The most notable are the Auger peaks, which are explained in terms of the decay of a more energetic electron to fill the vacant hole created by the x-ray photon, combined with the emission of an electron with an energy characteristic of the difference between the states involved in the process. The spectrum in Figure 2 includes a sequence of peaks labelled O KLL. These peaks represent the energy of the electrons ejected from the atoms due to the filling of the O 1s state (K shell) by an electron from the L shell coupled with the ejection of an electron from an L shell.
Figure 6: Elemental Silicon loss peaks and also x-ray satellite peak.
Less prominent than Auger lines are x-ray satellite peaks. Data acquired using a non-monochromatic x-ray source create satellite peaks offset from the primary spectral lines by the difference in energy between the resonances in the x-ray spectrum of the anode material used in the x-ray gun and also in proportion to the peaks in the x-ray spectrum for the anode material. Figure 6 indicates an example of a satellite peak to the primary Si 2p peak due to the use of a magnesium anode in the x-ray source. Note that Auger line energies are independent of the photon energy and therefore do not have satellite peaks.
Unlike the photoelectric peaks, the kinetic energy of the Auger lines is independent of the photon energy for the x-ray source. Since the kinetic energy of the photoelectrons are given in terms of the photon energy , the binding energy for the ejected electron and a work function by the relationship , altering the photon energy by changing the x-ray anode material causes the Auger lines and the photoelectric lines to move in energy relative to one another.
A further source for peaks in the background signal is due to resonant scattering of electrons by the surface materials. Plasmon
5
Copyright © 2013 Casa Software Ltd. www.casaxps.com
peaks for elemental silicon are also labelled on Figure 6. The sharpness of these plasmon peaks in Figure 6 is due to the nature of the material through which the photoelectrons must pass. For silicon dioxide, the loss structures are much broader and follow the trend of a typical XPS background signal. The sharp loss structures in Figure 6 are characteristic of pure metallic-like materials.
damage) and/or differential charging of the surface (localised differences in the charge-state of the surface).
Basic Quantification of XPS Spectra XPS counts electrons ejected from a sample surface when irradiated by x-rays. A spectrum representing the number of electrons recorded at a sequence of energies includes both a contribution from a background signal and also resonance peaks characteristic of the bound states of the electrons in the surface atoms. The resonance peaks above the background are the significant features in an XPS spectrum shown in Figure 7.
Figure 7: XPS and Auger peaks appear above a background of scattered electrons .
XPS spectra are, for the most part, quantified in terms of peak intensities and peak positions. The peak intensities measure how much of a material is at the surface, while the peak positions indicate the elemental and chemical composition. Other values, such as the full width at half maximum (FWHM) are useful indicators of chemical state changes and physical influences. That is, broadening of a peak may indicate: a change in the number of chemical bonds contributing to a peak shape, a change in the sample condition (x-ray Figure 8: Quantification regions
6
Copyright © 2013 Casa Software Ltd. www.casaxps.com
The underlying assumption when quantifying XPS spectra is that the number of electrons recorded is proportional to the number of atoms in a given state. The basic tool for measuring the number of electrons recorded for an atomic state is the quantification region. Figure 8 illustrates a survey spectrum where the surface is characterised using a quantification table based upon values computed from regions. The primary objectives of the quantification region are to define the range of energies over which the signal can be attributed to the transition of interest and to specify the type of approximation appropriate for the removal of background signal not belonging to the peak.
How to Compare Samples A direct comparison of peak areas is not a recommended means of comparing samples for the following reasons. An XPS spectrum is a combination of the number of electrons leaving the sample surface and the ability of the instrumentation to record these electrons; not all the electrons emitted from the sample are recorded by the instrument. Further, the efficiency with which emitted electrons are recorded depends on the kinetic energy of the electrons, which in turn depends on the operating mode of the instrument. As a result, the best way to compare XPS intensities is via, so called, percentage atomic concentrations. The key feature of these percentage atomic concentrations is the representation of the intensities as a percentage, that is, the ratio of the intensity to the total intensity of electrons in the measurement. Should the experimental conditions change in any way between measurements, for example the x-ray gun power output, then peak intensities would change in an absolute sense, but all else being equal, would remain constant in relative terms.
Relative Intensity of Peaks in XPS Each element has a range of electronic states open to excitation by the x-rays. For an element such as silicon, both the Si 2s and Si 2p transitions are of suitable intensity for use in quantification. The rule for selecting a transition is to choose the transition for a given element for which the peak area, and therefore in principle the RSF,
Figure 9: O 1s Region
7
Copyright © 2013 Casa Software Ltd. www.casaxps.com
is the largest, subject to the peak being free from other interfering peaks.
Quantification of the spectrum in Figure 8 requires the selection of one transition per element. Figure 9 illustrates the area targeted by the region defined for the O 1s transition; similar regions are defined for the C 1s, N 1s and Si 2p transitions leading to the quantification table displayed over the data in Figure 8. The Regions property page shown in Figure 10 provides the basic mechanism for creating and updating the region parameters influencing the computed peak area. Relative sensitivity factors are also entered on the Regions property page. The computed intensities are adjusted for instrument transmission and escape depth corrections, resulting in the displayed quantification table in Figure 8.
Transitions from different electronic states from the same element vary in peak area. Therefore, the peak areas calculated from the data must be scaled to ensure the same quantity of silicon, say, is determined from either the Si 2s or the Si 2p transitions. More generally, the peak areas for transitions from different elements must be scaled too. A set of relative sensitivity factors are necessary for transitions within an element and also for all elements, where the sensitivity factors are designed to scale the measured areas so that meaningful atomic concentrations can be obtained, regardless of the peak chosen.
Quantification regions are useful for isolated peaks. Unfortunately not all samples will offer clearly resolved peaks. A typical example of interfering peaks is any material containing both aluminium and copper. When using the standard magnesium or aluminium x-ray anodes, the only aluminium photoelectric peaks available for measuring the amount of aluminium in the sample are Al 2s and Al 2p. Both aluminium peaks appear at almost the same binding energy as the Cu 3s and Cu 3p transitions. Thus estimating the intensity of the aluminium in a sample containing these elements requires a means of modelling the data envelope resulting from the overlapping transitions illustrated in Figure 11.
Figure 10: Regions Property Page.
8
Copyright © 2013 Casa Software Ltd. www.casaxps.com
construct peak models. Figure 12 illustrates a spectrum where a thin layer of silver on silicon (University of Iowa, Jukna, Baltrusaitis and Virzonis, 2007, unpublished work) introduces an interference with the Si 2p transition from the Ag 4s transition.
Figure 11: Aluminium and Copper both in evidence at the surface.
Overlapping Peaks Techniques for modelling data envelopes not only apply to separating elemental information, such as the copper and aluminium intensities in Figure 11, but also apply to chemical state information about the aluminium itself. Intensities for the aluminium oxide and metallic states in Figure 11 are measured using synthetic line-shapes or components. An XPS spectrum typically includes multiple transitions for each element; while useful to identify the composition of the sample, the abundance of transitions frequently leads to interference between peaks and therefore introduces the need to
Figure 12: Elemental and oxide states of Silicon
9
Copyright © 2013 Casa Software Ltd. www.casaxps.com
The subject of peak-fitting data is complex. A model is typically created from a set of Gaussian/Lorentzian line-shapes. Without careful model construction involving additional parameter constraints, the resulting fit, regardless of how accurate a representation of the data, may be of no significance from a physical perspective. The subject of peak fitting XPS spectra is dealt with in detail elsewhere.
compensation for the sample and the availability of a peak at known binding energy to provide a reference for shifting the energy scale.
Peak models are created using the Components property page on the Quantification Parameters dialog window shown in Figure 13. A range of line-shapes are available for constructing the peak models including both symmetric and asymmetric functional forms. The intensities modelled using these synthetic line-shapes are scaled using RSFs and quantification using both components and regions are offered on the Report Spec property page of CasaXPS.
Peak Positions Figure 13: Components property page on the Quantification Parameters dialog window.
In principle, the peak positions in terms of binding energy provide information about the chemical state for a material. The data in Figure 2 provides evidence for at least three chemical states of silicon. Possible candidates for these silicon states might be SiO2, Si2O3, SiO, Si2O or Si, however an assignment based purely on the measured binding energies for the synthetic line-shapes relies on an accurate calibration for the energy scale. Further, the ability to calibrate the energy scale is dependent on the success of the charge
Charge Compensation The XPS technique relies on electrons leaving the sample. Unless these emitted electrons are replaced, the sample will charge relative to the instrument causing a retarding electric field at the sample surface. For conducting samples electrically connected to the instrument, the charge balance is easily restored; however, for
10
Copyright © 2013 Casa Software Ltd. www.casaxps.com
insulating materials electrons must be replaced via an external source. Insulating samples are normally electrically isolated from the instrument and low energy electrons and/or ions are introduced at the sample surface. The objective is to replace the photoelectrons to provide a steady state electrical environment from which the energy of the photoelectrons can be measured.
The data in Figure 14 shows spectra from PTFE (Teflon) acquired with and without charge compensation. The C 1s peaks are shifted by 162 eV between the two acquisition conditions, but even more importantly, the separation between the C 1s and the F 1s peaks differ between the two spectra by 5 eV. Without effective charge compensation, the measured energy for a photoelectric line may change as a function of kinetic energy of the electrons. Charge compensation does not necessarily mean neutralization of the sample surface. The objective is to stabilize the sample surface to ensure the best peak shape, whilst also ensuring peak separation between transitions is independent of the energy at which the electrons are measured. Achieving a correct binding energy for a known transition is not necessarily the best indicator of good charge compensation. A properly charge compensated experiment typically requires shifting in binding energy using the Calibration property page, but the peak shapes are good and the relative peak positions are stable. A nominally conducting material may need to be treated as an insulating sample. Oxide layers on metallic materials can transform a conducting material into an insulated surface. For example, aluminium metal oxidizes even in vacuum and a thin oxide layer behaves as an insulator. Calibrating spectra in CasaXPS is performed using the Calibration property page on the Spectrum Processing dialog window.
Figure 14: Insulating sample before and after charge compensation.
11
Copyright © 2013 Casa Software Ltd. www.casaxps.com
Depth Profiling using XPS
Figure 16: The set of O 1s spectra measured during a depth profiling experiment.
Figure 15: Segment of an XPS depth profile.
The set of XPS spectra corresponding to the oxygen 1s peaks from a depth profile experiment depicted logically in Figure 15 are displayed in Figure 16. The objective of these experiments is to plot the trend in the quantification values as a function of etch-time.
While XPS is a surface sensitive technique, a depth profile of the sample in terms of XPS quantities can be obtained by combining a sequence of ion gun etch cycles interleaved with XPS measurements from the current surface. An ion gun is used to etch the material for a period of time before being turned off whilst XPS spectra are acquired. Each ion gun etch cycle exposes a new surface and the XPS spectra provide the means of analysing the composition of these surfaces.
The actual depth for each XPS analysis is dependent on the etch-rate of the ion-gun, which in turn depends on the material being etched at any given depth. For example, the data in Figure 16 derives from a multilayer sample consisting of silicon oxide alternating with titanium oxide layers on top of a silicon substrate. The rate at which
12
Copyright © 2013 Casa Software Ltd. www.casaxps.com
the material is removed by the ion gun may vary between the layers containing silicon oxide and those layers containing titanium oxide, with a further possible variation in etch-rate once the silicon substrate is encountered. The depth scale is therefore dependent on characterizing the ion-gun however each XPS measurement is typical of any other XPS measurement, with the understanding that the charge compensation steady state may change between layers.
Figure 18: Logical structure of the VAMAS blocks in an XPS depth profile.
The XPS depth profile in Figure 17 is computed from the VAMAS file data logically ordered in CasaXPS as shown in Figure 18. The O 1s spectra displayed in Figure 16 are highlighted in Figure 18. One point to notice about the profile in Figure 17 is that the atomic concentration calculation for the O 1s trace is relatively flat for the silicon oxide and titanium oxide layers, in contrast to the raw data in Figure 16, where the chemically shifted O 1s peaks would appear to be more intense for the silicon oxide layers compared to the titanium oxide layers. This observation is supported by the plot of adjusted
Figure 17: XPS Depth Profile of silicon oxide/titanium oxide multilayer sample profiled using a Kratos Amicus XPS instrument.
13
Copyright © 2013 Casa Software Ltd. www.casaxps.com
peak areas in Figure 19, where again the O 1s trace is far from flat. The profile in Figure 17 is far more physically meaningful than the variations displayed in Figure 19. Normalization of the XPS intensities to the total signal measured on a layer by layer basis is important for understanding the sample. This example is a good illustration of why XPS spectra should be viewed in the context of the other elements measured from a surface.
Understanding Relative Sensitivity Factors for Doublet Transitions When quantifying XPS spectra, Relative Sensitivity Factors (RSF) are used to scale the measured peak areas so variations in the peak areas are representative of the amount of material in the sample surface. An element library typically contains lists of RSFs for XPS transitions. For some transitions more than one peak appears in the data in the form of doublet pairs and, in the case of the default CasaXPS library, three entries are available for each set of doublet peaks: one entry for the combined use of both doublet peaks in a quantification table and two entries for situations where only one of the two possible peaks are used in the quantification. A common cause of erroneous quantification is the inappropriate use of these optional RSF entries.
The details of how to analyze a depth profile in CasaXPS are discussed at length in The Casa Cookbook and other manual pages available from the Help option on the Help menu.
Figure 19: Peak areas scaled by RSF used to compute the atomic concentration plots in Figure 17.
Figure 20: Example of quantification regions and components used to quantify peak areas.
14
Copyright © 2013 Casa Software Ltd. www.casaxps.com
The data in Figure 20 are a set of high resolution spectra where quantification regions and components are used to calculate the area for the peaks. These data illustrate some of the issues associated with XPS quantification as the data includes singlet peaks in the form of O 1s, C 1s, Al 2s and N 1s; as well as doublet pairs: Cr 2p, Cu 2p, Ar 2p and Fe 2p. The spectra are sufficiently complex to involve overlaps such as the Al 2s and Cu 3s, while the Cu 2p1/2 peak includes signal from a Cr Auger line. When creating a table of percentage atomic concentrations it is important to select the correct RSF for the peak area chosen to measure the given element. Name Cr 2p 1/2 Cr 2p 3/2 Fe 2p 1/2 Fe 2p 3/2 Cu 2p 3/2 Al 2s Metal Al 2s Ox Ar 2p O 1s C1s N1s
R.S.F. 10.6041 10.6041 14.8912 14.8912 15.0634 0.753 0.753 2.65797 2.93 1 1.8
interference from other peaks and therefore simple integration regions can be used to measure the peak areas. The Ar 2p doublet peaks overlap each other; however the Cr 2p and Fe 2p peaks do not overlap, thus separate quantification regions are used to measure the area for these resolved doublet peaks. Even though separate regions are used to estimate the peak areas for the two peaks in each of the Cr 2p and the Fe 2p transitions, total RSFs for these transitions are used to scale the raw area calculated from the regions. Similarly, the total RSF is used to scale the Ar 2p doublet peaks, because both peaks from the doublet are used in calculating the peak area for argon. On the other hand, since the Cu 2p1/2 peak overlaps with the Cr LMM Auger transition, only the Cu 2p3/2 peak can be used with ease and so the reduced RSF must be applied to scale the peak area. The quantification table in Table 1 lists the regions and components used to calculate the atomic concentrations together with the RSFs for each transition.
% Conc. 2.9 6.2 2.2 4.5 4.4 61.4 5.1 5.5 6.2 1.5 0.2
Table 1: Quantification table showing RSFs used to scale the raw peak areas.
Note the peak model used to measure the Al 2s includes a component representing the contribution of the Cu 3s transition to the Al 2s spectrum in Figure 20. Copper is measured using the Cu 2p3/2 peak therefore the RSF for the Cu 3s component is set to zero so that the component does not appear in Table 1.
When measuring a transition, from the perspective of signal to noise, it is better to include both peaks from a doublet pair. For the data in Figure 20, the Fe 2p, Cr 2p and Ar 2p transitions are free of
By way of example, an alternative quantification regime might be to use only one of the two possible Fe 2p doublet peaks. The quantification in Table 2 removes the Fe 2p1/2 region from the
15
Copyright © 2013 Casa Software Ltd. www.casaxps.com
calculation by setting the RSF to zero, whilst adjusting the Fe 2p3/2 RSF to accommodate the absence of the Fe 2p1/2 peak area from the calculation. Since the ratio of 2p doublet peaks should be 2:1, the RSF for the Fe 2p3/2 region is two thirds of the total RSF used in Table 1. In Table 1, the percentage atomic concentration for Fe is split between the two Fe 2p doublet peaks, whereas in Table 2 the entire Fe 2p contribution is estimated using the Fe 2p3/2 and therefore the same amount of Fe is measured via either approach. A common misunderstanding is to use both peaks in the calculation, but still assign RSFs for the individual peaks in the doublet. The consequence of using both peaks and the specific RSFs to the individual peaks in the doublet is the contribution from Fe to the quantification table would be incorrectly increased by a factor of two.
R.S.F.
Cr 2p 1/2
10.6041
2.9
Cr 2p 3/2
10.6041
6.2
Fe 2p 3/2
9.8064
6.8
Cu 2p 3/2
15.0634
4.4
0.753
61.3
Al 2s Ox
0.753
5.1
Ar 2p
2.65797
5.5
O 1s
2.93
6.2
C1s
1
1.5
N1s
1.8
0.2
Table 2: Fe 2p 3/2 peak is used without the area from the Fe 2p 1/2.
To further illustrate the issues associated with the uses of the three RSFs associated with doublet peaks, consider the three possible options available when quantifying the Cr 2p doublet shown in Figures 21, 22 and 23. Table 3 shows that the corrected area when measured using any of these three options is approximately the same.
Note: the RSFs used in both Table 1 and Table 2 are Scofield crosssections adjusted for angular distribution corrections for an instrument with angle of 90º between the analyser and x-ray source. Name
Al 2s Metal
% Conc.
Figure 21: Intensity for Cr calculated from the Cr 2p1/2 transition.
16
Cr 2p1/2 RSF
Raw Area
3.60721
19234.8
Copyright © 2013 Casa Software Ltd. www.casaxps.com
RSF
Raw Area
Peak
Figure 22 Intensity for Cr calculated from the Cr 2p3/2 transition. Cr 2p3/2 RSF
Raw Area
6.9697
40871.9
Corrected Area Raw Area/(RSF*T*MFP)
Cr 2p 1/2
3.60721
19234.8
125.455
Cr 2p 3/2
6.9697
40871.9
138.192
Both Cr 2p Peaks
10.6041
60098.5
133.555
Table 3: Comparison of the intensities calculated from the three different combinations of peak area and RSF for the Cr 2p doublet illustrated in Figure 21 Figure 22 and Figure 23.
Electronic Energy Levels and XPS Peaks
Figure 23 Intensity for Cr calculated from both peaks in the doublet. Total RSF
Raw Area
10.6041
60098.5
An electron spectrum is essentially obtained by monitoring a signal representing the number of electrons emitted from a sample over a range of kinetic energies. The energy for these electrons, when excited using a given photon energy, depends on the difference
17
Copyright © 2013 Casa Software Ltd. www.casaxps.com
between the initial state for the electronic system and the final state. If both initial and final states of the electronic system are well defined, a single peak appears in the spectrum. Well defined electronic states exist for systems in which all the electrons are paired with respect to orbital and spin angular momentum. The initial state for the electronic system offers a common energy level for all transitions. When an electron is emitted from the initial state due to the absorption of a photon, the electrons emerge with kinetic energies characteristic of the final states available to the electronic system and therefore XPS peaks represent the excitation energies open to the final states. Since these final states include electronic sub-shells with unpaired electrons, the spin-orbit coupling of the orbital and spin angular moment results in the splitting of the energy levels otherwise identical in terms of common principal and orbital angular momentum. Thus, instead of a single energy level for a final state, the final state splits into two states referred to in XPS as doublet pairs. To differentiate between these XPS peaks, labels are assigned to the peaks based on the hole in the final state electronic configuration. Since these final states, even when split by spin-orbit interactions, are still degenerate in the sense that more than one electronic state results in the same energy for the system, three quantum numbers are sufficient to identify the final state for the xray excited system. Specifying the three quantum numbers in the format nlj both uniquely identifies the transition responsible for a
peak in the spectrum and offers information regarding the degeneracy of the electronic state involved. The relative intensity of these doublet pair peaks linked by the quantum numbers nl is determined from the j = l ± ½ quantum number. Doublet peaks appear with intensities in the ratio 2j1+1 : 2j2+1. Thus p-orbital doublet peaks are assigned j quantum numbers 1/2 and 3/2 and appear with relative intensities in the ratio 1:2.
Similar intensity ratios and differing energy separations are common features of doublet peaks in XPS spectra. Final states with s symmetry do not appear as doublets, e.g. Au 4s.
18
Copyright © 2013 Casa Software Ltd. www.casaxps.com
Examples of XPS Spectra
19
Copyright © 2013 Casa Software Ltd. www.casaxps.com
Bulk molybdenum disulphide measured using a Kratos Axis Nova
20
Copyright © 2013 Casa Software Ltd. www.casaxps.com
21
Copyright © 2013 Casa Software Ltd. www.casaxps.com
Tartaric Acid H
O
O H
C
C
O
H
H O
C
C H
O O H
Carbon appears in tartaric acid in two chemical environments resulting in two identifiable binding energies for the C 1s transition. Each chemical state appears in equal proportions in the tartaric acid molecule.
O H C C
C
O
C O
22
C
Copyright © 2013 Casa Software Ltd. www.casaxps.com
O
C
Oxygen appears in the tartaric acid molecule in two chemical environments resulting in two closely positioned binding energies for the O 1s transition. Each chemical state appears in a proportion of 2:4 in the tartaric acid molecule.
23
O H C
Copyright © 2013 Casa Software Ltd. www.casaxps.com
24
Copyright © 2013 Casa Software Ltd. www.casaxps.com
SiO2 measured using an aluminium anode.
25
Copyright © 2013 Casa Software Ltd. www.casaxps.com
Note the relative movement of the O KLL Auger line relative to the O 1s peak for data acquired using a magnesium anode compared to the SiO2 data measured with an aluminium anode. The elemental silicon in the sample also accounts for the sequence of plasmon loss peaks not seen in the SiO2 data.
26
Copyright © 2013 Casa Software Ltd. www.casaxps.com
Aluminium oxide sample analysed using an aluminium monochromatic source.
27
Copyright © 2013 Casa Software Ltd. www.casaxps.com
Again, metallic aluminium is responsible for the sequence of plasmon loss peaks associated with the Al 2p and Al 2s photoelectric lines not present in the aluminium oxide spectrum. It is worth observing the argon from the ion gun used to reduce the depth of the aluminium oxide layer exhibits plasmon loss structures characteristic of the aluminium metal. Note also that the plasmon loss peaks from the Al 2p transition will interfere with the Al 2s peak, hence the common practice of using the Al 2p line to quantify samples containing aluminium.
28
Copyright © 2013 Casa Software Ltd. www.casaxps.com
Gold measured using a silver anode in the x-ray monochromatic source.
29
Copyright © 2013 Casa Software Ltd. www.casaxps.com
Gold spectrum measured using a Cylindrical Sector Analyser (CSA) and Synchrotron a photon energy of 10.5 keV (PETRA P09 Beamline, Hamburg DESY; FOCUS HV-CSA).
30
Copyright © 2013 Casa Software Ltd. www.casaxps.com
31
Copyright © 2013 Casa Software Ltd. www.casaxps.com
32
Copyright © 2013 Casa Software Ltd. www.casaxps.com
33
Copyright © 2013 Casa Software Ltd. www.casaxps.com
34
Copyright © 2013 Casa Software Ltd. www.casaxps.com
35
Copyright © 2013 Casa Software Ltd. www.casaxps.com
36
Copyright © 2013 Casa Software Ltd. www.casaxps.com
37
Copyright © 2013 Casa Software Ltd. www.casaxps.com
38
Copyright © 2013 Casa Software Ltd. www.casaxps.com
39
Copyright © 2013 Casa Software Ltd. www.casaxps.com
40
Copyright © 2013 Casa Software Ltd. www.casaxps.com
41
Copyright © 2013 Casa Software Ltd. www.casaxps.com
42
Copyright © 2013 Casa Software Ltd. www.casaxps.com
43
Copyright © 2013 Casa Software Ltd. www.casaxps.com
44
Copyright © 2013 Casa Software Ltd. www.casaxps.com
45
Copyright © 2013 Casa Software Ltd. www.casaxps.com
46
Copyright © 2013 Casa Software Ltd. www.casaxps.com
47
Copyright © 2013 Casa Software Ltd. www.casaxps.com
Data provided by Bridget Rogers, Vanderbilt University, Nashville, TN, USA
48
Copyright © 2013 Casa Software Ltd. www.casaxps.com
49
Copyright © 2013 Casa Software Ltd. www.casaxps.com
50
Copyright © 2013 Casa Software Ltd. www.casaxps.com
51
Copyright © 2013 Casa Software Ltd. www.casaxps.com
52
Copyright © 2013 Casa Software Ltd. www.casaxps.com
53
Copyright © 2013 Casa Software Ltd. www.casaxps.com
54
Copyright © 2013 Casa Software Ltd. www.casaxps.com
55
Copyright © 2013 Casa Software Ltd. www.casaxps.com
56
Copyright © 2013 Casa Software Ltd. www.casaxps.com
The peak model is to illustrate a complex data envelope fitted with simple Gaussian-Lorentzian lineshapes. For a more complete discussion of Ce Oxide please see:V. Matolín, M. Cabala, V. Cháb, I. Matolínová, K. C. Prince, M. Škoda, F. Šutara, T. Skála and K. Veltruská, A resonant photoelectron spectroscopy study of Sn(Ox) doped CeO2 catalysts, Surf. Interface Anal. 40 (2008) 225–230.
57
Copyright © 2013 Casa Software Ltd. www.casaxps.com
58
Copyright © 2013 Casa Software Ltd. www.casaxps.com
59
Copyright © 2013 Casa Software Ltd. www.casaxps.com
60
Copyright © 2013 Casa Software Ltd. www.casaxps.com
61
Copyright © 2013 Casa Software Ltd. www.casaxps.com
62
Copyright © 2013 Casa Software Ltd. www.casaxps.com
XPS spectra and electronic structure of Group IA sulfates, M. Wahlqvist, A. Shchukarev / Journal of Electron Spectroscopy and Related Phenomena 156–158 (2007) 310–314 XPS Study of Group IA Carbonates, A.V. Shchukarev, D.V. Korolkov / CEJC 2(2) 2004 347-362
63
Copyright © 2013 Casa Software Ltd. www.casaxps.com
64
Copyright © 2013 Casa Software Ltd. www.casaxps.com
65
Copyright © 2013 Casa Software Ltd. www.casaxps.com
66
Copyright © 2013 Casa Software Ltd. www.casaxps.com
67
Copyright © 2013 Casa Software Ltd. www.casaxps.com
68
Copyright © 2013 Casa Software Ltd. www.casaxps.com
69
Copyright © 2013 Casa Software Ltd. www.casaxps.com
70
Copyright © 2013 Casa Software Ltd. www.casaxps.com
71
Copyright © 2013 Casa Software Ltd. www.casaxps.com
72
Copyright © 2013 Casa Software Ltd. www.casaxps.com
PMMA CH3 CH
C
n
2
C
O
O CH3
C C O
O
H
C
H
C
O H
C
C
C
H
H
C
C
H
C
H Different Chemical States for Carbon in Poly(methyl methacrylate)
C
C H
73
C
Copyright © 2013 Casa Software Ltd. www.casaxps.com
Poly(methyl methacrylate): C 1s peak assignments are based on those of Beamson and Briggs (The XPS of Polymers Database Edited by Graham Beamson and David Briggs (2000) ISNB: 0-9537848-4-3.
74
Copyright © 2013 Casa Software Ltd. www.casaxps.com
75
Copyright © 2013 Casa Software Ltd. www.casaxps.com
76
Copyright © 2013 Casa Software Ltd. www.casaxps.com
Acknowledgments Data used to prepare this PDF were donated by: University of Manchester, UK University of Nottingham, UK Peking University, China Max Plank Institute Düsseldorf, Germany Umeå University, Sweden Lehigh University, USA Vanderbilt University, Nashville, TN, USA Technical University of Eindhoven, The Netherlands University of Nantes, France and several unnamed contributors. A thank you to all involved in collecting these data.
77